Monotonous slope optimization DP

This optimization is also called "Convex Hull Trick" because it is either maintaining an upper convex hull ( decreasing slopes ) or a lower convex hull.
Also note that there are problems that do not necessarily have to be monotonous but still can be accelerated by maintaining slopes as convex hull, and the difference might come to that instead of deque, a binary search for slope and some quick insertions / deletions will be required ( Machine Works World Final 2011 pF ).
3709 -- K-Anonymous Sequence
POJ 3709 K-Anonymous Sequence
Given a non decreasing sequence of length n, you are allowed to make an operation: subtract 1 from any value in the sequence. Answer the minimum operations required to make each number in the new sequence appear k times.
2 ≤ k ≤ n ≤ 5e5, 0 ≤ a[i] ≤ 5e5
Let dp[ i ] = the minimum operations required to satisfy "K - Anonymous" conditions for the first i numbers
we can deduce the recursive relation
dp[ i ] = min{ dp[ j ] + ( a[ j + 1 ] - a[ j ] ) + ( a[ j + 2 ] - a[ j ] ) + ... + ( a[ i - 1 ] - a[ j ] ) } Ɐ 0 ≤ j ≤ i - k,
and consider S[ i ]: the prefix sum for the first i numbers in a,
we can transform the relation to
dp[ i ] = S[ i ] + min{ dp[ j ] - S[ j ] - a[ j ] * i + a[ j ] * j ) } Ɐ 0 ≤ j ≤ i - k,
and what the min{ ... } is really searching for, turns out to be a linear function for i
f[ j ]( i ) = -a[ j ] * i + C[ j ],
C[ j ] = dp[ j ] - S[ j ] + a[ j ] * j,
so we can actually think each of these f[ x ] as a line laying on a 2D plane.
When we would like to know the min function that lays along dp[ i ], we are to find the minimum y-coordinate for lines f[ j ] Ɐ 0 ≤ j ≤ i - k.
According to the description, we know that a is a non decreasing sequence, so we can deduce that the slope of these lines are monotonically decreasing ( and all negative ). Noticing that we can use a deque to maintain the upper convex hull, the total time complexity of the algorithm is O( N ).（絵がへたくそですみません)
We can see that the blue line has worse slope but its intercept is lower than the brown line, so it is always better than the brown before the intersection of the two lines. We will have to keep these kinds of brown lines that have potential.

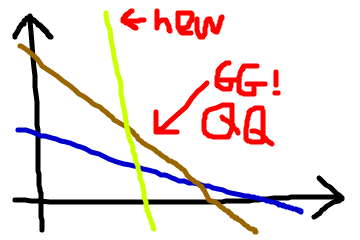
And this is when the brown line loses any chance at all to become part of the convex hull.

A method to find the brown line in this picture, given 3 lines f[ 1 ], f[ 2 ], f[ 3 ], sorted by the slope from large to small, let
f[ 1 ]( i ) = α[ 1 ] * i + β[ 1 ],
f[ 2 ]( i ) = α[ 2 ] * i + β[ 2 ],
f[ 3 ]( i ) = α[ 3 ] * i + β[ 3 ], α[ 1 ] ≥ α[ 2 ] ≥ α[ 3 ],
f[ 2 ] will never contain a point f[ 2 ]( i ) that is the minimum <=> ( α[ 2 ] - α[ 1 ] ) * ( β[ 3 ] - β[ 2 ] ) ≥ ( β[ 2 ] - β[ 1 ] ) * ( α[ 3 ] - α[ 2 ] ), ( someday later I will come back and prove for this ).

#include <cstdio>
#include <algorithm>
#include <deque>
using namespace std;
typedef long long ll;
const int MAXN = 5e5 + 5;

int n, k;
ll a[MAXN], pa[MAXN]; // pa: prefix sum of a
ll dp[MAXN];

struct line{
    ll slope, inter;
    line(ll _s, ll _i): slope( _s ), inter( _i ){}
    ll operator () (ll x){ return x * slope + inter; }
};

ll slope(int k){ return -a[k]; }
ll inter(int k){ return dp[k] - pa[k] + a[k] * k; }

bool check(line f1, line f2, line f3){
    ll a1 = f1.slope, b1 = f1.inter;
    ll a2 = f2.slope, b2 = f2.inter;
    ll a3 = f3.slope, b3 = f3.inter;
    return ( a2 - a1 ) * ( b3 - b2 ) >= ( b2 - b1 ) * ( a3 - a2 );
}

void solve(){
    for(int i = 0; i < n; ++i)
        pa[i + 1] = pa[i] + a[i];
    deque<line> dq;
    dq.push_back( line( slope( 0 ), inter( 0 ) ) );
    for(int i = k; i <= n; ++i){
        int j = i - k; // new line to consider
        if( j >= k ){ // if j < k, dp[j] = INF: impossible
            line newl( slope( j ), inter( j ) );
            while( dq.size() >= 2 && check( dq[ dq.size() - 2 ], dq[ dq.size() - 1 ], newl ) )
                dq.pop_back(); // if the back is the brown line we are talking about
            dq.push_back( newl ); // the yellow line comes in
        }
        while( dq.size() >= 2 && dq[0]( i ) >= dq[1]( i ) )
            dq.pop_front(); // goodbye if the front is no more competitive
        dp[i] = pa[i] + dq.front()( i );
    }
    printf("%lld\n", dp[n]);
}

int main(){
    int T; scanf("%d", &T);
    while( T-- ){
        scanf("%d %d", &n, &k);
        for(int i = 0; i < n; ++i)
            scanf("%lld", &a[i]);
        solve();
    }
    return 0;
}

SPOJ.com - Problem APIO10A
APIO10A - Commando
Given an array of integer, a1, a2 .. aN, N ≤ 1e6, 1 ≤ a[ i ] ≤ 100, now split this array to any much continuous segments. For each isolated array of integers, let its sum x, a * x * x + b * x + c credits will be given. Answer the maximum credits achievable. -5 ≤ a ≤ -1.
Let dp[ i ] = the maximum credits achievable with the first i numbers
we can deduce the recursive relation
dp[ i ] = max{ dp[ j ] + a * ( sum( a[ k ] Ɐ j < k ≤ i ) ^ 2 + b * ( sum( a[ k ] Ɐ j < k ≤ i ) + c } Ɐ 0 ≤ j < i,
and consider S[ i ]: the prefix sum for the first i numbers in a,
we can transform the relation to
dp[ i ] = C[ i ] + max{ slope[ j ] * S[ i ] + inter[ j ] } Ɐ 0 ≤ j < i,
C[ i ] = a * S[ i ] * S[ i ] + b * S[ i ] + c,
slope[ j ] = -2 * a * S[ j ],
inter[ j ] = dp[ j ] + a * S[ j ] * S[ j ] - b * S[ j ],
Notice that both x[ i ] ( = S[ i ] ) and slope[ j ] ( = -2 * a * S[ j ], a < 0 ), are strictly increasing monotonically, so after finishing query of an x[ i ], we can discard everything that is in the left of x[ i ], and this time we are maintaining a lower convex hull because the slope is increasing.

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN = 1e6 + 6;

struct line{
    ll slope, inter;
    line(ll _s, ll _i): slope( _s ), inter( _i ){}
    ll operator () (ll x){ return x * slope + inter; }
};

int n;
ll a, b, c;
ll p[MAXN]; // p[i]: sum of ther first i numbers
ll dp[MAXN];

ll x(int i){ return p[i]; }
ll slope(int i){ return -2 * a * p[i]; }
ll inter(int i){ return a * p[i] * p[i] - b * p[i] + dp[i]; }
ll C(int i){ return a * p[i] * p[i] + b * p[i] + c; }

bool check(line f1, line f2, line f3){
    ll a1 = f1.slope, b1 = f1.inter;
    ll a2 = f2.slope, b2 = f2.inter;
    ll a3 = f3.slope, b3 = f3.inter;
    return ( a2 - a3 ) * ( b2 - b1 ) >= ( a1 - a2 ) * ( b3 - b2 );
}

void solve(){
    deque<line> dq;
    dq.push_back( line( slope( 0 ), inter( 0 ) ) );
    for(int i = 1; i <= n; ++i){
        while( dq.size() >= 2 && dq[0]( x(i) ) < dq[1]( x(i) ) )
            dq.pop_front();
        dp[i] = dq[0]( x(i) ) + C( i );
        line newl( slope( i ), inter( i ) );
        while( dq.size() >= 2 && check( dq[ dq.size() - 2 ], dq[ dq.size() - 1 ], newl ) )
            dq.pop_back();
        dq.push_back( newl );
    }
    printf("%lld\n", dp[n]);
}

int main(){
    int T; scanf("%d", &T);
    while( T-- ){
        scanf("%d", &n);
        scanf("%lld %lld %lld", &a, &b, &c);
        for(int i = 0; i < n; ++i){
            int x; scanf("%d", &x);
            p[i + 1] = p[i] + x;
        }
        solve();
    }
    return 0;
}