CFR 631 E. Product Sum ( Convex hull trick DP )

Problem - E - Codeforces
pekempeyさんの記事と公式の editorialよりいい解釈はないと思うのでとりあえず。
pekempey.hatenablog.com
Editorial Codeforces Round #344 (Div. 2) - Codeforces
For this problem, we will consider convex hull trick. There are 2 things we will do for each index when traversing, we will update the line of the characteristic of the current index as a usable function, and we will query for the all the usable functions for the maximum f( x ). Since the slope is monotonically increasing, all the popping and pushing lines will be done in the back. Suppose L1 = a1x + b1, L2 = a2x + b2, L3 = a3x + b3 and a1 < a2 < a3, we will not need L2 iff for all x, L2( x ) < L1( x ) OR L2( x ) < L3( x ) satisfies, since it will never be the maximum. Maintaining the usable functions well with this property, we will create a lower convex hull, which will give us opportunity to make fast queries for maximum f( x ). For some x, if the global maximum value in all lines is f_g( x ), f_i( x ) ≤ f_g( x ) ≤ f_j( x ) will satisfy for all i < g and g < j, thus we can apply binary search to find such g.

For how to judge whether L2 is a bad line, we can suppose the intercept of L1 and L3 be ( α, β ), it will be that for all x < α, a1x + b1 > a2x + b2, and for all α < x, a3x + b3 > a2x + b2, carefully moving around the inequality, we will have ( b2 - b3 ) * ( a2 - a1 ) ≤ ( b1 - b2 ) * ( a3 - a2 ).

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2e5 + 5;
const int MAXA = 1e6 + 6;
typedef long long ll;

template <class T>
void upmax(T &x, T v){ if( x < v ) x = v; }

int n;
int a[ MAXN ];
ll pa[ MAXN ];
ll org; // orignal score
ll max_delta; // maximum difference after operation

struct line{
    ll a, b; // ax + b = y
    line(ll _a = 0, ll _b = 0): a(_a), b(_b){}
    ll operator() (ll x){ return a * x + b; }
};

struct ConvexHull{
    deque<line> dq;
    ConvexHull(){}
    bool isBad(line f1, line f2, line f3){
        return ( f2.b - f3.b ) * ( f2.a - f1.a ) <= ( f1.b - f2.b ) * ( f3.a - f2.a );
    }
    void addLine(line f){
        while( dq.size() >= 2 && isBad( dq[ dq.size() - 2 ], dq[ dq.size() - 1 ], f ) )
            dq.pop_back();
        dq.push_back( f );
    }
    ll qmax(ll x){
        int lb = -1, rb = dq.size() - 1;
        while( lb + 1 < rb ){
            int mid = lb + rb >> 1;
            if( dq[ mid ]( x ) <= dq[ mid + 1 ]( x ) )
                lb = mid;
            else
                rb = mid;
        }
        return dq[ rb ]( x );
    }
} ch0, ch1;

int main(){
    ios::sync_with_stdio( false );
    cin >> n;
    for(int i = 1; i <= n; ++i){
        cin >> a[ i ];
        pa[ i ] = pa[ i - 1 ] + a[ i ];
        org += (ll)a[ i ] * i;
    }
    for(int i = 2; i <= n; ++i){
        ch0.addLine( line( i - 1, -pa[ i - 2 ] ) );
        upmax( max_delta, ch0.qmax( a[ i ] ) + pa[ i - 1 ] - (ll)a[ i ] * i );
    }
    for(int i = n - 1; i >= 1; --i){
        ch1.addLine( line( -( i + 1 ), -pa[ i + 1 ] ) );
        upmax( max_delta, ch1.qmax( -a[ i ] ) + pa[ i ] - (ll)a[ i ] * i );
    }
    cout << org + max_delta << endl;
    return 0;
}

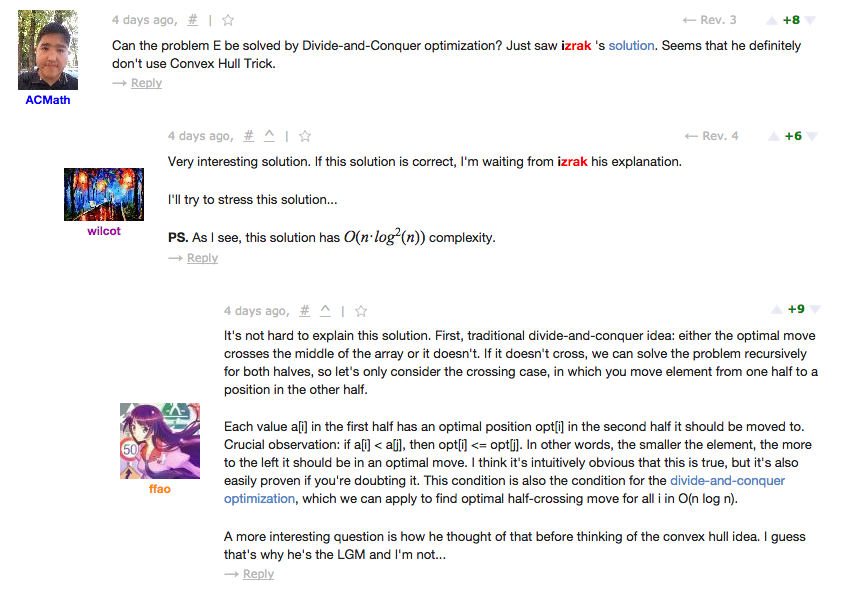
Looks like divide and conquer approach will work as well, in O( n lg n )
Submission #16526854 - Codeforces