CFR 806 B. Dynamic Problem Scoring ( Dummy Constraints, Greedy )

Problem - B - Codeforces

題意：
有 N 個人參加比賽，有五題，每個人的參數是五題的答對時間，沒有答對則以 -1 表示。一個人在一個題目的得分是這樣計算的：
考慮一個題，令 p 為答對人數，q 為參賽人數，則 p / q 對應到表格中的該題的最大分數。

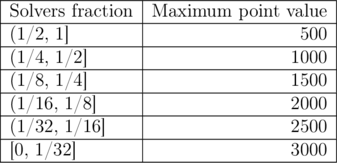
對於一個沒有答對這題的人，他的得分是 0。
否則令他的答對時間為 x，他的得分是 max_score * ( 1 - x / 250 )。
你是編號 1 號的選手，你希望你的總分嚴格大於編號 2 號的選手。
你有 1e9 + 7 個假帳號，你希望用最少的假帳號改變局勢，使得你的願望滿足。
對於每一題你可以選擇是否用假帳號答題，注意，你無法用假帳號答你本身沒有答對的題。
輸出最少需要的帳號數量，若不可能則輸出 -1。

制約：
The first line contains a single integer n (2 ≤ n ≤ 120) — the number of round participants, including Vasya and Petya.
Each of the next n lines contains five integers ai, 1, ai, 2..., ai, 5 ( - 1 ≤ ai, j ≤ 119) — the number of minutes passed between the beginning of the round and the submission of problem j by participant i, or -1 if participant i hasn't solved problem j.
It is guaranteed that each participant has made at least one successful submission.
Vasya is listed as participant number 1, Petya is listed as participant number 2, all the other participants are listed in no particular order.

解法：
首先考慮如果你已經決定要派 x 個假帳號出場，那對於一題會選擇答或不答，這個很容易搞定，詳細看 calc() 函數。
這題的要點在於，要發現當人數超過 4000 的時候，在貪心策略下，局勢完全不會改變。
雖然裝得很像單調函數，但它不是。

時間 / 空間複雜度：
O( 5000 )

#include <bits/stdc++.h>
using namespace std;

int N;
int A[ 120 ][ 5 ];
int correct[ 5 ];

int score( int a, int p, int q ) {
  if( a == -1 ) return 0;
  if( 32LL * p <= q ) {
    return 3000 - 3000 / 250 * a;
  } else if( 16LL * p <= q ) {
    return 2500 - 2500 / 250 * a;
  } else if( 8LL * p <= q ) {
    return 2000 - 2000 / 250 * a;
  } else if( 4LL * p <= q ) {
    return 1500 - 1500 / 250 * a;
  } else if( 2LL * p <= q ) {
    return 1000 - 1000 / 250 * a;
  }
  return 500 - 500 / 250 * a;
}

int calc( int p ) {
  int f = 0;
  for( int i = 0; i < 5; ++i ) {
    if( A[ 0 ][ i ] == -1 ) {
      f += score( A[ 0 ][ i ], correct[ i ], N + p )
         - score( A[ 1 ][ i ], correct[ i ], N + p );
    } else if( A[ 1 ][ i ] == -1 or A[ 0 ][ i ] < A[ 1 ][ i ] ) {
      f += score( A[ 0 ][ i ], correct[ i ], N + p )
         - score( A[ 1 ][ i ], correct[ i ], N + p );
    } else {
      f += score( A[ 0 ][ i ], correct[ i ] + p, N + p )
         - score( A[ 1 ][ i ], correct[ i ] + p, N + p );
    }
  }
  return f;
}

signed main() {
  cin >> N;
  for( int i = 0; i < N; ++i ) {
    for( int j = 0; j < 5; ++j ) {
      cin >> A[ i ][ j ];
      correct[ j ] += A[ i ][ j ] > -1;
    }
  }
  for( int i = 0; i <= 5000; ++i ) {
    if( calc( i ) > 0 ) {
      cout << i << endl;
      exit( 0 );
    }
  }
  cout << -1 << endl;
  return 0;
}